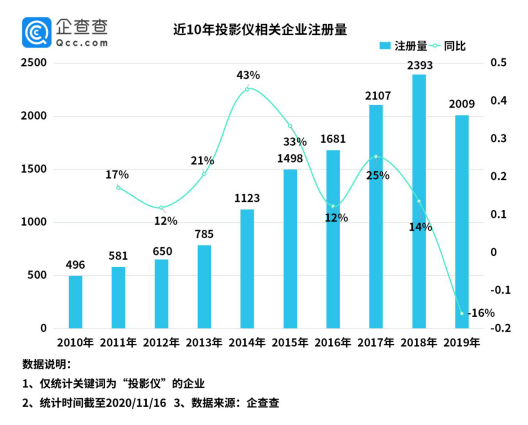
ж–Үз« жҸ’еӣҫ
еҰӮеӣҫзӨә,第дәҢиЎҢж”ҫзҡҮеҗҺзҡ„дҪҚзҪ®еҸӘиғҪд»Һ第дёүдёӘж јеӯҗејҖе§ӢйҖү
第дәҢиЎҢжҲ‘们йҖү第дёүдёӘж јеӯҗж”ҫзҡҮеҗҺпјҢйҖүе®ҢејҖе§ӢеңЁз¬¬дёүиЎҢйҖүпјҢ第дёүж–№еҸҜйҖүзҡ„дҪҚзҪ®д№ҹеҸ—еҲ°дәҶ第дёҖпјҢдәҢиЎҢзҡҮеҗҺжүҖж”ҫдҪҚзҪ®зҡ„еҪұе“Қ

ж–Үз« жҸ’еӣҫ
еҰӮеӣҫзӨәпјҢ第дёүиЎҢеҸӘиғҪд»Һ第дә”дёӘж јеӯҗејҖе§Ӣж”ҫзҪ®зҡҮеҗҺ
еҗҢзҗҶпјҢ第дёүпјҢеӣӣпјҢдә”иЎҢйғҪд»Һе·ҰеҲ°еҸійҖүжӢ©з¬ҰеҗҲжқЎд»¶зҡ„зҡ„ж јеӯҗж”ҫзҪ®зҡҮеҗҺпјҢйҖүе®ҢеҗҺй—®йўҳжқҘдәҶпјҢ第е…ӯиЎҢжүҖеңЁиЎҢжІЎжңүеҸҜйҖүзҡ„дҪҚзҪ®дәҶпјҒеҰӮеӣҫзӨә

ж–Үз« жҸ’еӣҫ
жҖҺд№ҲеҠһе‘ўпјҢеӣһжәҜпјҒйҮҚж–°ж‘Ҷж”ҫ第дә”иЎҢзҡ„зҡҮеҗҺпјҢе°Ҷе…¶ж”ҫеҲ°з¬¬е…«ж јдёҠ

ж–Үз« жҸ’еӣҫ
йҮҚж–°ж‘Ҷж”ҫеҗҺеҸ‘зҺ°з¬¬е…ӯиЎҢиҝҳжҳҜжІЎжңүз¬ҰеҗҲжқЎд»¶зҡ„ж јеӯҗпјҢе’ӢеҠһпјҢжҲ‘们зҹҘйҒ“第е…ӯиЎҢеҸҜж‘Ҷж”ҫзҡҮеҗҺзҡ„ж јеӯҗеҸ—第дә”иЎҢеҪұе“ҚпјҢиҖҢ第дә”иЎҢеҸ—第еӣӣиЎҢж‘Ҷж”ҫзҡҮеҗҺдҪҚзҪ®зҡ„еҪұе“Қзҡ„пјҢжүҖд»ҘеӣһжәҜеҲ°з¬¬еӣӣиЎҢпјҢе°ҶзҡҮеҗҺдҪҚзҪ®ж‘Ҷж”ҫеҲ°еҪ“еүҚиЎҢзҡ„е…¶д»–дҪҚзҪ®пјҲ第дёғж јпјүпјҢеҶҚжҺҘзқҖеҫҖдёӢж”ҫ 5пјҢ6пјҢ7пјҢ8 иЎҢзҡ„зҡҮеҗҺ гҖӮгҖӮгҖӮпјҢеҸӘиҰҒдёҚж»Ўи¶іжқЎд»¶пјҢж”№еҸҳдёҠдёҖеұӮзҡ„зҡ„жқЎд»¶йҮҚж–°жқҘпјҢдёҠдёҖеұӮи°ғж•ҙеҗҺиҝҳжҳҜдёҚз¬ҰеҗҲжқЎд»¶пјҢеҶҚи°ғж•ҙдёҠдёҠеұӮзҡ„ гҖӮгҖӮгҖӮпјҢи°ғж•ҙе®ҢеҗҺйҮҚж–°еҫҖдёӢйҖ’еҪ’йҖүжӢ©пјҢзӣҙеҲ°жүҫеҲ°з¬ҰеҗҲжқЎд»¶зҡ„пјҢжүҫеҲ°д№ӢеҗҺеҶҚеңЁз¬¬дёҖеұӮжҚўдёҖдёӘдҪҚзҪ®йҖүзҡҮеҗҺйҖ’еҪ’еҫҖдёӢеұӮйҖүжӢ©жү§иЎҢпјҢзӣҙеҲ°жүҫеҲ°жүҖжңүзҡ„и§ЈпјҢиҝҷз§ҚдёҚж»Ўи¶іжқЎд»¶е°ұеӣһйҖҖдёҠеұӮи°ғж•ҙеҶҚиҜ•зҡ„жҖқжғіе°ұжҳҜеӣһжәҜжі•пјҢеҸҜд»ҘзңӢеҲ°еӣһжәҜжі•дёҖиҲ¬жҳҜз”ЁйҖ’еҪ’е®һзҺ°зҡ„ гҖӮ
еӣһжәҜз®—жі•жңүдёҚе°‘еҸҳз§ҚпјҢиҝҷйҮҢжҲ‘们йҮҚзӮ№д»Ӣз»ҚдҪҝз”ЁдҪҚиҝҗз®—зҡ„еӣһжәҜз®—жі•пјҢе®ғжҳҜжүҖжңүи§Јжі•дёӯжңҖй«ҳж•Ҳзҡ„пјҒеҰӮжһңеңЁйқўиҜ•дёӯиғҪдҪҝз”ЁдҪҚиҝҗз®—жқҘи§ЈеӣһжәҜз®—жі•пјҢз»қеҜ№дјҡи®©йқўиҜ•е®ҳз»ҷдҪ дёӘеӨ§еӨ§зҡ„иөһпјҒ
жҺҘдёӢжқҘжҳҜйҮҚзӮ№дәҶпјҢжҖҺд№Ҳз”ЁдҪҚиҝҗз®—жқҘжұӮи§Ј гҖӮ
еңЁд»ҘдёҠеӣһжәҜжі•зҡ„еҲҶжһҗдёӯпјҢжҲ‘们дёҚйҡҫеҸ‘зҺ°пјҢеңЁе…«зҡҮеҗҺй—®йўҳдёӯпјҢй—®йўҳзҡ„е…ій”®жҳҜжүҫеҮәиЎҢеҸҜж”ҫзҡҮеҗҺзҡ„ж јеӯҗ гҖӮжүҫеҲ°д№ӢеҗҺй—®йўҳе°ұи§ЈеҶідәҶ 90%пјҢжүҖд»ҘжҺҘдёӢжқҘжҲ‘们е°ұжқҘзңӢзңӢжҖҺд№ҲжүҫиҝҷдәӣеҸҜз”Ёзҡ„ж јеӯҗ гҖӮ
еҒҮи®ҫжҲ‘们иҰҒжұӮ解第дёүиЎҢеҸҜж”ҫзҡҮеҗҺзҡ„ж јеӯҗпјҲиҜҙжҳҺдёҖдәҢиЎҢзҡ„зҡҮеҗҺе·Іж”ҫеҘҪдәҶпјүйӮЈд№Ҳ第дёүиЎҢеҸҜж”ҫзҡҮеҗҺзҡ„дҪҚзҪ®еҸ—еҲ°е“ӘдәӣжқЎд»¶зҡ„йҷҗеҲ¶е‘ў гҖӮжҳҫ然еңЁз¬¬дёҖдәҢиЎҢе·Іж”ҫзҡҮеҗҺзҡ„ж јеӯҗжүҖеңЁзҡ„еҲ—пјҢе·Ұж–ңзәҝпјҢеҸіж–ңзәҝеҜ№еә”зҡ„ж–№ж јйғҪдёҚиғҪж”ҫзҡҮеҗҺпјҢеҰӮеӣҫзӨә:

ж–Үз« жҸ’еӣҫ
жҲ‘们д»Ҙ column жқҘи®°еҪ•жүҖжңүдёҠж–№иЎҢе·Іж”ҫзҪ®зҡ„зҡҮеҗҺеҜјиҮҙеҪ“еүҚиЎҢж јеӯҗдёҚеҸҜз”Ёзҡ„йӣҶеҗҲпјҢжүҖеңЁеҲ—еҰӮжһңж”ҫдәҶзҡҮеҗҺпјҢеҲҷеҪ“еүҚиЎҢж јеӯҗеҜ№еә”зҡ„дҪҚзҪ®дёә 1пјҢеҗҰеҲҷдёә 0пјҢеҗҢзҗҶ,д»Ҙ pieпјҲж’ҮпјҢе·Ұж–ңзәҝпјү и®°еҪ•жүҖжңүе·Іж”ҫзҪ®зҡ„зҡҮеҗҺе·Ұж–ңж–№еҗ‘еҜјиҮҙеҪ“еүҚиЎҢж јеӯҗдёҚеҸҜз”Ёзҡ„йӣҶеҗҲпјҢnaпјҲжҚәпјҢеҸіж–ңзәҝпјү иЎЁзӨәжүҖжңүе·Іж”ҫзҪ®зҡ„зҡҮеҗҺеҸіж–ңж–№еҗ‘еҜјиҮҙеҪ“еүҚиЎҢдёҚеҸҜз”Ёзҡ„йӣҶеҗҲ гҖӮеҲҷеҜ№дәҺ第дёүиЎҢжқҘиҜҙжҲ‘们жңүпјҡ
column = 10010000 (дёҠеӣҫдёӯзҡ„第дёҖдёӘеӣҫпјҢ第 1пјҢ4 еҲ—ж”ҫдәҶзҡҮеҗҺпјҢжүҖд»Ҙ 1пјҢ4 дҪҚзҪ®дёә 1пјҢе…¶д»–дҪҚзҪ®дёә 0пјүе°ҶиҝҷдёүдёӘеҸҳйҮҸдҪңжҲ–иҝҗз®—еҫ—еҲ°з»“жһңеҰӮдёӢ
pie = 00100000 (дёҠеӣҫдёӯзҡ„第дәҢдёӘеӣҫпјҢе·Ұж–ңзәҝз»ҸиҝҮ第дёүиЎҢзҡ„第дёүдёӘж–№ж јпјҢжүҖд»Ҙ第дёүдҪҚдёә 1пјү
na = 00101000 (дёҠеӣҫдёӯзҡ„第дёүдёӘеӣҫпјҢеҸіж–ңзәҝз»ҸиҝҮ第дёүиЎҢзҡ„第дёү, дә”дёӘж–№ж јпјҢжүҖд»Ҙ第дёү,дә”дҪҚдёә 1пјү
10010000д№ҹе°ұжҳҜиҜҙеҜ№дәҺ第дёүеұӮжқҘиҜҙ第 1пјҢ3пјҢ4пјҢ5 дёӘж јеӯҗдёҚиғҪж”ҫзҡҮеҗҺ гҖӮеҰӮеӣҫзӨә
| 00100000
| 00101000
-----------------------
10111000

ж–Үз« жҸ’еӣҫ
дәҺжҳҜеҸҜзҹҘ column | pie | na еҫ—еҲ°зҡ„з»“жһңдёӯеҖјдёә 0 зҡ„д»ЈиЎЁеҪ“еүҚиЎҢеҜ№еә”зҡ„ж јеӯҗеҸҜж”ҫзҡҮеҗҺпјҢ1 д»ЈиЎЁдёҚиғҪж”ҫпјҢдҪҶжҲ‘们жғіж”№жҲҗ 1 д»ЈиЎЁж јеӯҗеҸҜж”ҫзҡҮеҗҺпјҢ0 д»ЈиЎЁдёҚеҸҜж”ҫзҡҮеҗҺпјҢжҜ•з«ҹиҝҷж ·жӣҙз¬ҰеҗҲжҲ‘们зҡ„жҖқз»ҙж–№ејҸпјҢжҖҺд№ҲеҠһпјҢеҸ–еҸҚдёҚе°ұиЎҢдәҶпјҢдәҺжҳҜжҲ‘们жңү~(column| pie | na) гҖӮ
й—®йўҳжқҘдәҶпјҢиҝҷж ·еҸ–еҸҚжҳҜжңүй—®йўҳзҡ„пјҢеӣ дёәиҝҷдёүдёӘеҸҳйҮҸйғҪжҳҜе®ҡд№үзҡ„ int еһӢпјҢдёә 32 дҪҚпјҢеҸ–еҸҚд№ӢеҗҺй«ҳдҪҚзҡ„ 0 е…ЁйғЁеҸҳжҲҗдәҶ 1пјҢиҖҢжҲ‘们еҸӘжғідҝқз•ҷдҪҺ 8 дҪҚпјҲеӣ дёәжҳҜ 8 зҡҮеҗҺпјүпјҢжғіжҠҠй«ҳдҪҚйғҪзҪ®дёә 0пјҢжҖҺд№ҲеҠһпјҢиҝҷйҮҢе°ұиҰҒз”ЁеҲ°дҪҚиҝҗз®—зҡ„黑科жҠҖдәҶ
~(column | pie | na) & ((1 << 8)-1)еҗҺйқўзҡ„зҡ„ ((1<< 8) -1) иЎЁзӨәе…ҲжҠҠ 1 еҫҖе·Ұ移 8 дҪҚпјҢеҖјдёә 100000000,еҶҚеҮҸ 1 пјҢеҲҷдҪҺ 8 дҪҚе…ЁйғЁдёә 1пјҢй«ҳдҪҚе…ЁйғЁдёә 0пјҒпјҲеҚі 0011111111пјүеҶҚдҪңдёҺиҝҗз®—пјҢеҚіеҸҜдҝқз•ҷдҪҺ 8 дҪҚпјҢеҺ»йҷӨй«ҳдҪҚ гҖӮ
иҙ№дәҶиҝҷд№ҲеӨ§зҡ„еҠІпјҢжҲ‘们з»ҲдәҺжҠҠеҪ“еүҚиЎҢеҸҜж”ҫзҡҮеҗҺзҡ„ж јеӯҗйғҪжүҫеҮәжқҘдәҶпјҲжүҖжңүдҪҚеҖјдёә 1 зҡ„ж јеӯҗеҸҜж”ҫзҪ®зҡҮеҗҺпјү гҖӮжҺҘдёӢжқҘжҲ‘们еҸӘиҰҒеҒҡдёӘеҫӘзҺҜпјҢйҒҚеҺҶжүҖжңүдҪҚдёә 1 зҡ„ж јеӯҗпјҢжҜҸж¬ЎеҸ–еҮәеҸҜз”Ёж јеӯҗж”ҫдёҠзҡҮеҗҺпјҢеҶҚжүҫдёӢдёҖеұӮеҸҜж”ҫзҪ®зҡҮеҗҺзҡ„ж јеӯҗпјҢдҫқжӯӨйҖ’еҪ’дёӢеҺ»еҚіеҸҜ,зӣҙеҲ°жүҖжңүиЎҢйғҪйҒҚеҺҶе®ҢжҜ•пјҲйҖ’еҪ’зҡ„з»ҲжӯўжқЎд»¶пјү гҖӮ
жҺЁиҚҗйҳ…иҜ»
- йҳҝйҮҢзҡ„еһғеңҫжҖҺд№Ҳеӣһ收пјҹJava G1жәҗз ҒеҲҶжһҗдёҺи°ғдјҳжүӢеҶҢ
- иҝҗеҠЁе‘ҳ|马永ејәпјҡиҒҢдёҡйҖүжүӢдёҺдёҡдҪҷйҖүжүӢзҡ„еҢәеҲ«
- иҢ¶дёҺеҷЁзӣёжҝЎд»ҘжІ«,йҷҲзҡ®е’Ңжҷ®жҙұиҢ¶зҶҹиҢ¶зҡ„е®ҢзҫҺжҗӯй…Қ
- иҢ¶еӯҗеҝғжіЎж°ҙе–қзҡ„дҪңз”Ё,е–қиғ–еӨ§жө·зҡ„зҰҒеҝҢдёҺдҪңз”Ё
- еҚҒжӢӣж•ҷдҪ еҲ¶дҪңиҜұдәәеҶ°иҢ¶
- иҢ¶еҸ¶иө·жәҗзҡ„е°Ҹж•…дәӢ,й«ҳеҸӨз‘ҷиҢ¶зҡ„иө·жәҗдёҺзҺҜеўғ
- дёӯеӣҪе”җеҲҖе’Ңж—Ҙжң¬еҲҖжңүдҪ•еҲҶеҲ«пјҹ?е”җеҲҖдёҺж—Ҙжң¬еҲҖе“ӘдёӘжӣҙејәпјҹ
- еҚ•дҪҚдёҚз»ҷејҖзҰ»иҒҢиҜҒжҳҺжҖҺд№ҲеҠһпјҹ
- дәӢдёҡеҚ•дҪҚиҒҳз”ЁеҗҲеҗҢжңҹж»ЎпјҢеҚ•дҪҚжҳҜеҗҰеҝ…йЎ»з»ӯзӯҫ
- й«ҳй“Ғеә§дҪҚжңүABCDFпјҢдёәе•ҘжІЎжңүEпјҹ